Quick Links
ILRS Overview
Satellite Laser Ranging (SLR) and Lunar Laser Ranging (LLR) use short-pulse lasers and state-of-the-art optical receivers and timing electronics to measure the two-way time of flight (and hence distance) from ground stations to retroreflector arrays on Earth orbiting satellites and the Moon. Scientific products derived using SLR and LLR data include precise geocentric positions and motions of ground stations, satellite orbits, components of Earth’s gravity field and their temporal variations, Earth Orientation Parameters (EOP), precise lunar ephemerides and information about the internal structure of the Moon. Laser ranging systems are already measuring the one-way distance to remote optical receivers in space and can perform very accurate time transfer between sites far apart. Laser ranging activities are organized under the International Laser Ranging Service (ILRS) which provides global satellite and lunar laser ranging data and their derived data products to support research in geodesy, geophysics, Lunar science, and fundamental constants. This includes data products that are fundamental to the International Terrestrial Reference Frame (ITRF), which is established and maintained by the International Earth Rotation and Reference Systems Service (IERS). The ILRS develops the necessary global standards/specifications for laser ranging activities and encourages international adherence to its conventions.
The Role of the ILRS in Earth Science
The ILRS is one of the space geodetic services of the International Association of Geodesy (IAG) and is a member of the IAG’s Global Geodetic Observing System (GGOS). The Services, under the umbrella of GGOS, provide the geodetic infrastructure necessary for monitoring global change in the Earth system (Beutler and Rummel, 2012).
Space Geodesy and Earth Science Research

The Jason-2 satellite uses an on-board altimeter to monitor global sea surface height (Courtesy NASA/JPL-Caltech)
Planet Earth is very dynamic and as a result, natural hazards disrupt our lives, cause havoc, and levy great costs on society. The surface of Earth is in constant motion at a variety of time scales. In the "solid Earth" we see the motion of the tectonic plates, the rebound due to the melting of the continental ice sheets from the last Ice Age (c.f. Yoder, 1983; Rubincam, 1984; Tamisea et al., 2007; Holger and Wu, 2011; Whitehouse et al., 2012), co-seismic and post seismic deformation due to earthquakes (e.g., Hreinsdottir et al., 2003; Ozawa et al., 2011), deformation associated with volcanic inflation and deflation (e.g., Baker and Amelung, 2012; Aly and Cochran, 2011), periodic motions due to solid Earth and ocean tides and the load exerted by the oceanic motion due to ocean tides. The polar ice caps (Greenland, Antarctica), ice sheets (Alaska and Patagonia) and other mountain glacier systems around the world are losing mass (Jacob et al., 2012; Shepherd et al., 2012) which results in further unloading of the crust as well as an addition of fresh water in the oceans that raises mean sea level. The change in ocean height (as measured by satellite-based ocean radar altimeters and coastal tide gauges) includes both the effect of additional mass, dilation of the ocean water due to thermal expansion as the oceans heat up, and the deformation of the ocean bottoms due to post-glacial rebound (Leuliette and Willis, 2011). The instantaneous ocean surface is thus a reflection of many phenomena including ocean tides, currents, tsunamis, weather and mass exchange with water sources on land (e.g. Ray, 1999; Lyard et al., 2006; Knudsen et al., 2011; Albertella et al., 2012; Boening et al., 2011).
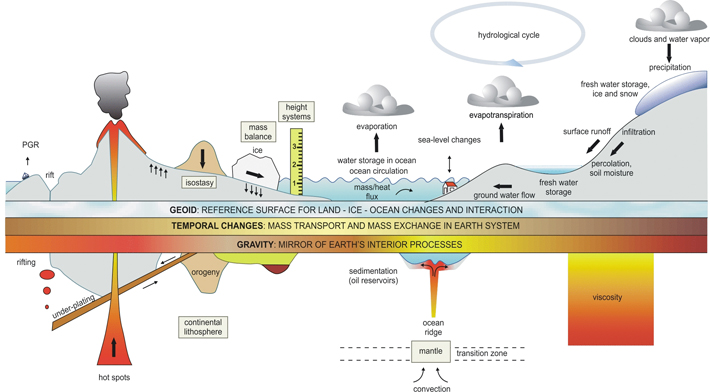
The interrelation of gravity, gravity variations, mass transport and distribution. (GFZ, 2005). Reference: "Mass Transport and Mass Distribution in the Earth System" p. 4, http://www.massentransporte.de/fileadmin/Dokumente/programmschrift-Ed2.pdf
The dynamics of the atmosphere and the oceans are strongly coupled and this is reflected in the observed structure of Earth rotation. Space geodetic geometric techniques like SLR provide tools to measure these phenomena and their temporal changes; ground-based and space-based gravimetric techniques provide independent tools to help us understand how mass is moving around in Earth’s fluid envelope. The more accurate and comprehensive the measurements, the better we will understand the nature of these global phenomena, how they are linked, how they change in time and how they affect our lives. Measurements allow us to model the effects and to forecast their evolution, but even more important, they form the scientific basis on which long-term actions can be planned and reasonable policies can be adopted such that they will allow us to better contend with current trends and future conditions.
The Reference Frame and the Role of Co-location

NASA's Next Generation SLR system, NGSLR, located at NASA GSFC.
Common threads in these measurements are the reference frame and precision orbit determination (POD).
The reference frame provides the stable coordinate system that allows us to measure change (link measurements) over space (thousands of kilometers), time (decades and even generations), and evolving technology. It is defined by an accurate, stable set of ground station positions and their linear velocities, in a global network of co-located space geodetic "Core Sites" including SLR, VLBI, GNSS, and DORIS where available (Altamimi et al., 2011). Other sites with lower levels of co-location and technology play a key role in densifying the network and enhancing global coverage.
The reason for the co-location is that each of the techniques makes its measurement in a different way and thus each measures parameters a little differently and is affected by a different set of systematic errors (e.g., Pearlman et al., 2002; Altamimi and Collilieux, 2009; Dow et al., 2009; Boeckmann et al., 2010; Valette et al., 2010; Schuh and Behrend, 2012). Each technique has different strengths and weaknesses, and the combination (through co-location) allows us to take advantage of the strengths and mitigate the weaknesses of each. An essential element in this combination is the accurate determination of the inter-technique vectors (vector ties at each site). These are determined through very accurate ground surveys between accessible instrument reference points and then careful extrapolation and modeling to the inaccessible system invariant points (Sarti et al., 2004).
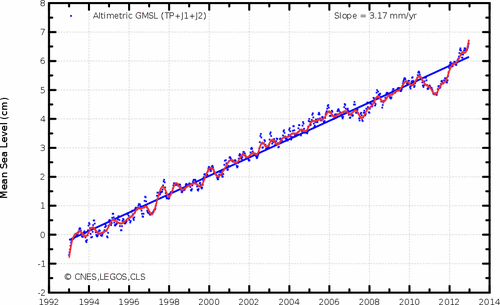
Global mean sea level (GMSL) rise from altimetry missions (seasonal effects filtered). (Credits CLS/CNES/Legos). For an up-to-date version see: http://www.aviso.oceanobs.com/en/news/ocean-indicators/mean-sea-level/
The most stringent requirement for the reference frame comes from monitoring sea level change; observations suggest it is rising at an average rate of about 3 mm per year with annual variations that are not well understood. With the current uncertainty in the reference frame (Earth center of mass, scale, EOP, etc.) at the 10 mm level, it is not clear whether or not other effects are influencing our measurements. The improved GGOS reference frame of 1-mm measurement accuracy with 0.1-mm/yr. precision will be required to convincingly address the sea level change issue and other Earth systems processes that are not far behind. This will require a more comprehensive global network of well distributed "core sites" with state-of-the-art technology of co-located SLR, VLBI, GNSS, and DORIS where available. In addition, a more dense network of GNSS stations would be necessary to distribute the reference frame globally to users anywhere on Earth interested in geo-locating their measurements in this frame at any time. Further details on GGOS are given in Plag, H-P, Pearlman, M., 2009.

Laser retroreflector on the Moon.
The primary targets used in determining the positions of the ITRF sites and their motions are artificial satellites, the Moon, and quasars. A prerequisite in the use of artificial satellites (replacing the stars of the astronomical observations) is the accurate knowledge of their orbits, governed by the laws of physics and the precise modeling of geophysical phenomena that perturb their orbits by exerting additional forces on them.
The POD process allows us to accurately model the conservative and non-conservative forces affecting a satellite's orbital motion and simultaneously improve our models for the underlying phenomena to better understand the source behind those forces (c.f. Marshall et al., 1995; Cerri et al., 2010; Lemoine et al., 2010). POD is also essential for calibration, validation, and proper interpretation of the data from space-borne measurement systems such as altimeters that map ocean and ice surfaces – we need to know the height of the satellite in order to know the height of the mapped surface. Here again, co-location of techniques ensures the robustness of the estimated surface heights.
Co-location of techniques takes place not only at ground stations, but also on satellites. Many of the satellites with active measuring systems aboard have two or three tracking techniques. This combination has provided orbits with cm level accuracy to support altimetry and other active satellite-borne remote sensing systems. Space-borne co-location will help strengthen the overall network combination, in particular through ranging to the GNSS constellations.
The Ground Network of Core Sites to Meet the GGOS Requirements
Studies have been conducted as part of a U.S. National Research Council panel review process to scope the size of the required network to meet the GGOS requirements. The NRC panel concluded that the network will need approximately 30 globally distributed, well positioned, co-located sites with modern technology and proper operating conditions; about half of these "Core Sites" must track a complex of GNSS satellites with SLR to calibrate the GNSS orbits which will be the means by which the ITRF will be distributed to the public. This network would continue to be augmented by lesser co-location stations to augment global coverage. Simulations continue to better understand the dependence of the space geodesy data products on system and network parameters.
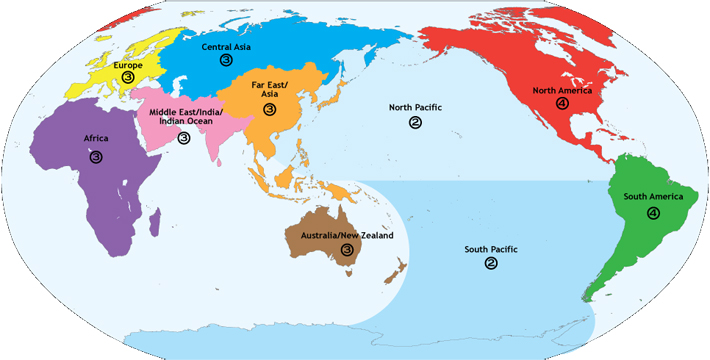
Proposed global network coverage for future space geodesy site locations.
There are presently ten core sites in operation; several more are in testing or construction. Most of these sites have legacy technology, but in many cases upgrades are underway or planned. Unfortunately these sites do not represent an optimum global distribution. A concerted international effort will be required to add additional stations to enhance global distribution, expand co-location sites into Core Sites, and to deploy new technology at current and future sites.
Laser Ranging and the Path Forward

The satellite and lunar laser ranging station "MeO" in Grasse, France
The path forward to improve ground system performance is known and being pursued by practitioners with each technique (ILRS Technology web page, 2012 International Technical Laser Workshop). Newer SLR systems are using higher pulse repetition rates (0.1 – 2 KHz) for faster data acquisition; smaller, faster slewing telescopes for more rapid target acquisition and pass interleaving; capabilities to ranging from Low Earth Orbiting (LEO) satellites to the Earth navigation satellites; more accurate pointing for greater link efficiency; narrower laser pulse widths for greater precision; new detection systems for greater ranging accuracy; greater temporal, spatial, and spectral filtering for improved signal to noise conditions; more automation for operational economy (24/7) and greater temporal coverage; and modular construction and more off-the-shelf components for lower fabrication/operations/maintenance cost.
Laser ranging has long been a tool to study lunar science and fundamental constants (Ciufolini and Pavlis, 2004); it has now been expanded to receivers in space for time transfer, improved spacecraft ephemerides, and planetary science. The contribution of SLR to the establishment and maintenance of the reference frame relies on the core of geodetic satellites including LAGEOS-1 and -2, Etalon-1 and -2, and the newly added LARES satellite. Additions of similar geodynamic satellites will add further strength; studies are underway to establish if Starlette and Stella can add strength to this constellation. Work continues on more efficient arrays with narrower satellite signatures to improve ranging accuracy by limiting systematic errors. Improvements have been proposed to the design of the GNSS laser retroreflector arrays (LRA) (see Dell'Agnello et al.).

Laser ranging station in Shanghai, China
Facilities are now available that can accurately characterize array properties, examine different array design options, optimize designs, and set specifications. Several groups are designing and building improved LRA’s, and new satellites with such arrays are being planned. The foreseen near-future improvements in the SLR/LLR ground and space segments promise a more accurate product from a more efficient network.
References:
- Albertella A., R. Savcenko, T. Janjic et al. (2012), High resolution dynamic ocean topography in the southern ocean from GOCE, Geophysical Journal International, 190(2), 922-930, doi: 10.1111/j.1365-246X.2012.05531.x.
- Altamimi Z., X. Collilieux, and L. Métivier (2011), ITRF2008: an improved solution of the international terrestrial reference frame, J. Geodesy, 85(8), 457-473, doi:10.1007/s00190-011-0444-4.
- Altamimi Z., X. Collilieux, IGS contribution to ITRF, Journal of Geodesy, vol. 83, number 3-4, page 375-383, doi:10.1007/s00190-008-0294-x, 2009.
- Aly M.H. and E.S. Cochran (2011), Spatio-temporal evolution of Yellowstone deformation between 1992 and 2009 from InSAR and GPS observations. Bulletin of Volcanology, 73(9), doi: 10.1007/s00445-011-0483-y.
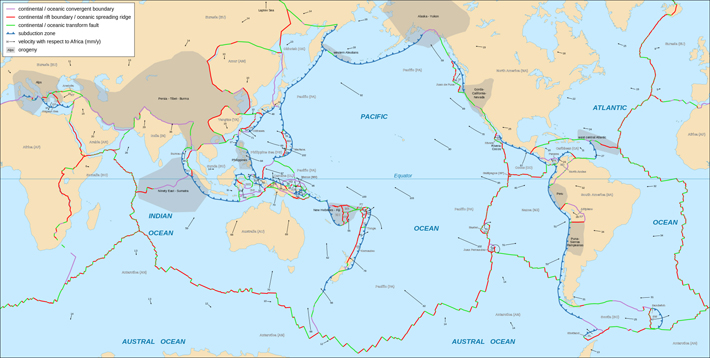
- Argus D., R.G. Gordon, and C. DeMets (2011), Geologically current motion of 56 plates relative to the no-net rotation frame, Geochemistry, Geophysics, Geosystems, 12(11), doi:1029/2011GC003751.
- Baker S. and F. Amelung (2012), Top-down inflation and deflation at the summit of Kilauea Volcano, Hawaii observed with InSAR, J. Geophys. Res.-Solid Earth, 117(B12406), doi: 10.1029/2011JB009123.
- Beutler, G. and R. Rummel (2012), Scientific rationale and development of the Global Geodetic Observing System, in International Association of Geodesy Symposia, Volume: 136, pp. 987-993, S.C. Kenyon, M.C. Pacino, U.J. Marti editors, Springer-Verlag, doi: 10.1007/978-3-642-20338-1_123.
- Bird P. (2003), An updated digital model of plate boundaries, Geochemistry, Geophysics, Geosystems, 4(3), doi:10.1029/2001GC000252.
- Boeckmann S., T. Artz, and A. Nothnagel (2010), VLBI reference frame contributions to ITRF2008, J. Geodesy, 84(3), 201-219, doi:10.1007/s00190-009-0357-7.
- Boening C., J.K. Willis, F.W. Landerer et al., The 2011 La Niña: So strong, the oceans fell, Geophys. Res. Lett.
- Cerri L., J.P. Berthias, W.I. Bertiger et al. (2010), Precision orbit determination standards for the Jason series of altimeter missions, Marine Geodesy, 33(1), 379-418, doi: 10.1080/01490419.2010.488966.
- Ciufolini, I., Pavlis, E.C., "A confirmation of the general relativistic prediction of the Lense-Thirring effect", Nature, Vol. 431, pp. 958-960, 2004.
- Dell’Agnello, S., et al, Creation of the new industry-standard space test of laser retroreflectors for the GNSS and LAGEOS, J. Adv. Space Res. 47 (2011) 822–842. Published on the second of two "Galileo Special Issues" titled Scientific Applications of Galileo and other Global Navigation Satellite Systems – II, on March 1, 2011. Posted by ILRS among its "ILRS Related Reports".
- Dell’Agnello, S. et al., ETRUSCO-2, an ASI-INFN Project for the development and SCF-Test of GNSS laser retroreflector arrays, Proceedings of the "3rd International Colloquium Scientific and Fundamental Aspects of the Galileo Programme", Copenhagen, Aug. 31 - Sep. 2, 2011 published by ESA. Upon ESA's indication, ILRS posted this paper by ILRS on its Galileo webpage.
- Dow J.M., R.E. Neilan, and C. Rizos (2009), The International GNSS Service in a changing landscape of Global Navigation Satellite Systems, J. Geodesy, 83(3-4), 191-198, doi: 10.1007/s00190-008-0300-3.
- Holger S. and P. Wu (2011), Glacial isostatic adjustment in Fennoscandia- A review of data and modeling, Journal of Geodynamics, 52(3-4), 169-204, doi:10.1016/j.jog.2011.03.02.
- Hreinsdottir S., J.T. Freymueller, H.J. Fletcher, et al. (2003), Coseismic slip distribution of the 2002 M(w)7.9 Denali fault earthquake, Alaska, determined from GPS measurements, Geophys. Res. Lett. 30(13), 1670, doi:10.1029/2003GL017447.
- Jacob T., J. Wahr, W.T. Pfeffer, S. Swenson (2012), Recent contributions of glaciers and ice caps to sea level rise, Nature, 482 (7386), 514-518, doi: 10.1038/nature10847.
- Knudsen P., R. Bingham, O. Andersen, M.H. Rio (2011), A global mean dynamic topography and ocean circulation estimation using a preliminary GOCE gravity model, J. Geodesy, 85(11), 861-879, doi: 10.1007/s00190-011-0485-8.
- Lemoine F.G., N.P. Zelensky, D.S. Chinn, et al. (2010), Towards development of a consistent series for TOPEX, Jason-1 and Jason-2, Adv. Space Res., 46(12), 1513-1540, doi: 10.1016/j.asr.2010.05.007.
- Leuliette, E.W., and J.K. Willis (2011), Balancing the sea level budget, Oceanography 24(2), 122–129, doi:10.5670/oceanog.2011.32.
- Lyard, F., F. Lefèvre, T. Letellier and O. Francis. Modelling the global ocean tides: a modern insight from FES2004, Ocean Dynamics, 56, 394-415, 2006.
- Marshall J.A., N.P. Zelensky, S.M. Klosko, et al. (1995), The temporal and spatial characteristics of TOPEX/Poseidon radial orbit error, J. Geophys. Res., 100(C12), 25331-25352, doi: 10.1029/95JC01845.
- Ozawa, S., Nishimura T, Suito, H. et al., Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake, Nature, 475(7356), 373-U123, doi:10.1038/nature10227.
- Pearlman M.R, J.J. Degnan, and J.M. Bosworth, The international laser ranging service, Adv. Space Res., 30(2), 135-143, doi:10.1016/S0273-1177(02)00277-6.
- Plag, H.-P. and Pearlman, M., Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020, Eds. Springer 2009. p. 332.
- Ray, R. D. (1999), A Global ocean tide model from TOPEX/Poseidon altimetry: GOT99.2, NASA/TM-1999-209478.
- Rubincam, D.P. (1984), Post-glacial rebound observed by LAGEOS and the effective viscosity of the lower mantle, J. Geophys Res., 89(NB2), 1077-1087, doi: 10.1029/JB089iB02p01077.
- Sarti, P., P. Sillard, and L. Vittuari (2004), Surveying co-located space geodetic instruments for ITRF computation, J. Geodesy, 78(3), 210-222, doi: 10.1007/s00190-004-0387-0.
- Schuh H. and D. Behrend (2012), VLBI: A fascinating technique for geodesy and astrometry, Journal of Geodynamics, 61, 68-80, doi: 10.1016/j.jog.2012.07.007.
- Shepherd A., E. Ivins, A Geruo, et al., A reconciled estimate of ice-sheet mass balance, Science, 338(6111), 1183-1189, doi:10.1126/science.1228102.
- Tamisea M.E., J.X. Mitrovica, and J. L. Davis (2007), GRACE gravity data constrain ancient ice geometries and continental dynamics over Laurentia, Science, 316(5826), 881-883, doi:10.1126/science.1137157.
- Valette J.J., F.G. Lemoine, P. Ferrage et al. (2010), The IDS contribution to ITRF2008, Adv. Space Res., 46(12), 1614-1632, doi: 10.1016/j.asr.2010.05.029.
- Whitehouse P.L., M.J. Bentley, G.A. Milne, et al. (2012), A new glacial isostatic model for Antarctica, calibrated and tested using measurements of relative sea level change and present-day uplift rates, Geophysical Journal International, 190(3), 1464-1482, doi:10.1111/j.1365-246X.2012.05557.x.
- Yoder, C.F., J.G. Williams, J.O. Dickey et al. (1983), Secular variation of the Earth harmonic J2 coefficient from LAGEOS, and nontidal acceleration of Earth rotation, Nature, 303(5920), 757-762, doi: 10.1038/303757a0.






